How the Predicted Observables for Exoplanets are Calculated
The Predicted Observables for Exoplanets (POE) tool calculates habitable zone radii, predicted insolation, and predicted radial velocity, astrometric, and transit signatures for archived and user-specified objects. The equations used for these calculations are detailed below.
Luminosity
If the stellar luminosity, L*, is not provided explicitly as an input (either from user input parameters for a custom stellar signature, or from the Archive for a table query), then it is derived from the stellar effective temperature, Teff , and stellar radius, R* (if available):
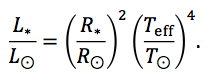
Habitable Zone
We use a simplified definition for Habitable Zone (HZ) following that used by NASA's Exoplanet Exploration Program Office. The inner and outer boundaries are defined using the (optimistic) "recent Venus" and "early Mars" models, respectively, from Kasting et al. 1993. For a Sun-like (G2) star, these are given at 0.75 and 1.77au. We scale these values for stellar luminosity, and neglect any dependency on stellar effective temperature (effectively assuming the planet albedo is constant with wavelength). We define the HZ "center" as 1au for Earth around the Sun, and likewise scale with stellar luminosity:
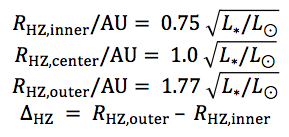
where RHZ represents the various habitable zone radii, and ΔHZ is the habitable zone width. If a value for the distance, d, to the system is available, then the radii and width are also calculated in angular units as seen on the sky:
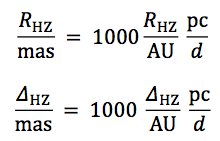
Planet Signatures
Maximum Projected Separation
The maximum projected separation on the sky of a planet-star pair, for a circular orbit, is a function of the distance to the system, d, and the semi-major axis, a, both in meters. In arcsec:
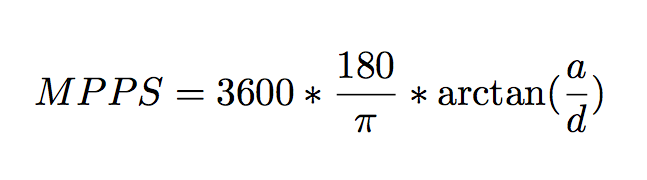
Orbital Period
Where the planet's orbital period, P, is needed, it is calculated using Kepler's third law from the planet semi-major axis, a, and the stellar mass, M* :

Note that this form of the equation assumes that the planet mass, Mp, is negligible in comparison to the stellar mass (Mp << M*).
Insolation Flux
Given the stellar luminosity (either explicitly provided, or derived as above), the insolation (power per unit area), S, in Earth units, is given directly by the inverse square law:

Radial Velocity Semi-amplitude
The predicted radial velocity semi-amplitude, K, depends on the planet period, P, planet mass, Mp, the stellar mass, M*, the orbital inclination, i, and the orbital eccentricity, e. We use the following expression to obtain K in ms-1 :

where the numerical constants include appropriate unit conversions. Currently we fix the eccentricity at zero, and an inclination of 90° is assumed for the "Earth-like" and "Jupiter-like" input options. The equation is similar to eqn. 2 of Cumming et al. 1999, but takes the period in days, retains the eccentricity, and avoids the approximation that Mp << M*. An outline of the full derivation of the RV semi-amplitude can be found in "The Exoplanet Handbook," Perryman, 2011.
Astrometric Semi-Amplitude
The astrometric amplitude of the wobble of a host star induced by its companion in au is derived straightforwardly from balance of the star/planet system about its center of mass. The distance to the system then determines the angular size of the projected motion on the sky. Assuming a circular orbit, the host star describes an ellipse on the sky whose angular semi-major axis, Δθ, is given by:

where the numerical coefficients again reflect the appropriate unit conversions.
Transit Depth
The predicted transit depth, δ, is given by the ratio of the projected area of the planet to that of the star. In percent:
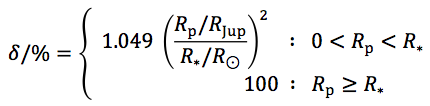
where the numerical factor, 1.049, comes from converting Rp and R* to the same units, with a further factor of 100 to convert to percent. For the case where a planet is larger than its host, the transit depth is capped at 100%.
References
Cumming, A., Marcy, G. W., & Butler, R. P. 1999, ApJ, 526, 890 Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 Perryman, M. 2011, The Exoplanet Handbook, Cambridge University Press, New York; ISBN: 0521765595
Last updated: 2 November 2016




