How the Ephemerides are Calculated
- The Ephemeris
- Planet Model Parameters
- Visible transits
- Date Conversion
- Differences from transitsearch.org
The calculation of the transit ephemerides is based on an algorithm developed by Greg Laughlin of UC Santa Cruz. The NASA Exoplanet Archive development staff has updated and extended the algorithm, utilizing various IPAC tools to provide the service.
The algorithm is linear and comprised of a small number of steps:
- The first step in performing the calculation is to assemble the appropriate data. The data are retrieved from the NASA Exoplanet Archive's databases, and may be superceded by any parameters input into the Custom Parameters interface. These parameters include planetary and stellar data, and information on transit properties, for example:
- Planet name (e.g., "55 Cnc b")
- Orbital Period
- Orbital Period Uncertainty
- Epoch of periastron passage
- Uncertainty in periastron epoch
- Planet orbital eccentricity
- Longitude of periastron
- Semiamplitude of the radial velocity (if known, for planet not known to transit)
- Stellar mass (for model)
- Planet radius
- Stellar radius
- Right ascension and declination
- Transit duration (if known)
- Transit duration uncertainties
- Transit midpoint
- Transit midpoint uncertainties
- An ephemeris may be computed by one of two means, either through knowledge of the planet's orbital elements and planetary and stellar radii, or via a known transit midpoint epoch and duration time.
- Once the necessary inputs are collected, the algorithm
determines whether any parameters are missing. If using the orbital elements, two of these
parameters, the planetary radius and semimajor axis, may be produced
via planetary properties models, if missing; see the section below
on Planet Model Parameters for more.
If other parameters are unavailable, the service will notify you.
- Next, the ephemeris is computed:
- Transit Midpoint Method: Since the transit midpoint is known, the algorithm simply iterates over the period, including uncertainties, such that
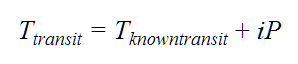
- For example, for the beginning of the window:
- We also propogate through the uncertainty on the predicted transit midpoint. Similarly to the time of transit, the uncertainty on the time of transit is calculated by:
- Epoch of Periastron: The planet's orbital position is determined by finding the time since periastron passage.
- Given the longitude of periastron, ω, compute the true anomaly ƒ = π/2 - ω, assuming that the true longitude Θ = π/2.
- Compute the eccentric anomaly E,
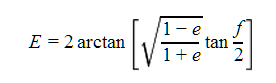
- Finally, compute the time since periastron passage,
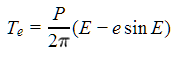 where P is the period, and e is the eccentricity. Note that the term in parentheses is Kepler's equation, which has been substituted for the mean anomaly.
where P is the period, and e is the eccentricity. Note that the term in parentheses is Kepler's equation, which has been substituted for the mean anomaly.
- Compute the transit duration:
- Compute the change in true anomaly due to the transit,
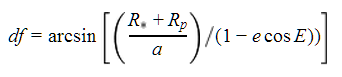
- Compute the adjusted true anomaly, ƒ + dƒ.
- Compute the adjusted eccentric anomaly Ε, as in the first equation in this section.
- Compute the transit duration, tT = PM/π where M is the mean anomaly, M= Ε - e sinΕ.
- The time of central transit is computed inside the loop by iterating over periods, given the time of periastron passage Tperi and the time since passage Te, such that
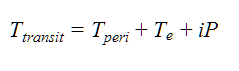
where i is the loop index.
The early and late transits, however, are not computed by simply subtracting or adding half the transit duration time td from the now-known time of central transit. Instead, the periastron passage times are first computed from the orbital elements,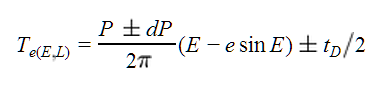
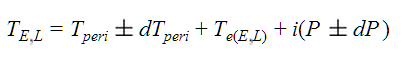
- Get the planet mass m sin i >1 from the radial velocity K by iteration, until q > 1:
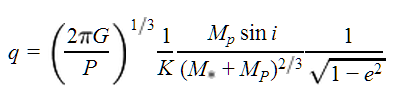
where G is Newton's constant, P is the period, K is the radial velocity semiamplitude, Mpis the planet mass, M* is the stellar mass, and e is the eccentricity (see, e.g., Kane 2007 Eq. 2). Since the algorithm assumes sin i = 1, this gives Mp directly. - Compute semimajor axis a,
- Compute the effective temperature,
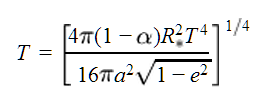
- Compute the radius estimate by interpolating over a table of model parameters containing planet temperature and density information, returning a fiducial radius if necessary.
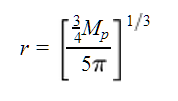
- You can generate ephemerides showing past and predicting future transits, from 1858 to 2406.
-
Geometric transit probabilities are computed, rather than its convolution with an observing window, thereby removing any location bias. - Data are available both from the NASA Exoplanet Archive's databases and user-generated input, allowing you real-time access to the latest available observational data, as well as the opportunity to use proprietary input or observed data.
- Visible transits can be predicted for any location on Earth, allowing you to schedule time at an observatory or prepare grant proposals.
- You can produce ephemerides for planets with either orbital elements or with known transit midpoints.
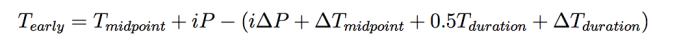
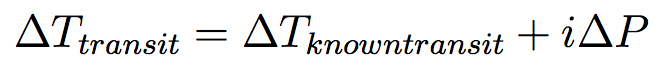
Planet Model Parameters
This section describes the algorithm that estimates the semimajor axis and planetary radius. Inputs to this routine include the planetary albedo α (assumed to be 0.2), eccentricity, tidal quality factor Qp (assumed to be 1000000), semiamplitude of the radial velocity K, period, stellar mass, effective temperature, stellar radius, and relative orbital inclination factor sin i=1.
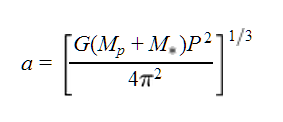
Determining Whether Transits Are Visible
To determine whether an exoplanet is observable by a terrestrial observer, you must ensure that the observation time occurs during the specified observation location and time, while the planet is favorably above the horizon. The Solar Position Algorithm of Reda & Albert (2003) accomplishes this task. Next, the observer's latitude and longitude are converted into altitude and azimuth, and the values are compared. If the Sun is ten degrees below the horizon, and the planet is 20 degrees above the horizon at the time of central transit, then the service deems the central transit observable and it is then listed in the table. A more sophisticated determination of visibility involving a determination of airmass is in development.
Date Conversion
Date conversion between Julian and calendar systems is well-documented, for example in Montenbruck (1989) and Murray & Dermott (1999). We follow the latter here.
The following algorithm is used to convert a Julian Date to a calendar date. (See Murray, C.D., Dermott, S.F., Solar System Dynamics, Cambridge University Press, Cambridge, 1999, for the algorithm upon which this process is based.)
To convert a Julian date to a calendar date, you need to define the following quantities:
| a | = int[JD+0.5] | |
| b | = int [(a-1867216.25)/36524.25] | if a ≥ 2299161 |
| c | = a+1524 | if a < 2299161 |
| c | = a + b - int[b/4]+1525 | if a ≥ 2299161 |
| d | = int[(c-122.1)/365.25] | |
| e | = int[365.25/d] | |
| f | = int[(c-e)/30.6001] |
where the function int[x] denotes the largest whole number less than or equal to (x). The calendar date is given by
| D | = c - e - int[30.6001f] + frac[JD + 0.5] |
| M | = f - 1 - 12[int(f/14)] |
| Y | = d - 4715 - int[(7 + M)/10] |
where frac[x] denotes the fractional part of x.
The conversion from calendar to Julian date uses the same method as specified in Murray, C.D., Dermott, S.F., Solar System Dynamics, Cambridge University Press, Cambridge, 1999. Given a calendar year (Y), month (M), day (D), and Universal Time (UT), define the auxiliary quantities y and m by
| y | = Y - 1 | and | m | = M + 12 | M ≤ 2 | |
| y | = Y | and | m | = M | M > 2 |
and the quantity B by
| B | = -2 | up to and including 4 Oct 1582 |
| B | = int[y/400] - int[y/100] | from and including 15 Oct 1582 |
where int[x] is as above. Then, the Julian date is
Differences from transitsearch.org
There are a few differences between the ephemeris calculation used here and that used by Greg Laughlin's transitsearch.org:
Last Updated: 22 September 2016




